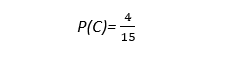در درسهای مجموعهها، مفاهیم پایهای از جعبههای ریاضی را بررسی میکنیم که به کمک آنها میتوانیم مسائل پیچیدهتری را حل کنیم. در این فصل، با مجموعهها، نحوهی تعریف، نمایش، و ویژگیهای آنها آشنا خواهیم شد. این مفاهیم شامل انواع مجموعهها، نحوهی مقایسه مجموعهها، اجتماع، اشتراک، تفاضل، و احتمال است. در ادامهی مباحث مجموعه کمک درسی پایه نهم، در این مقاله علاوه بر توضیح کامل درس، نمونه سوال فصل اول ریاضی نهم با جواب و مثالهایی از صفحات ۴، ۱۰، ۱۶، ۱۷ در اختیارتان قرار میگیرد.
درس اول: معرفی مجموعهها
مجموعه چیست؟ نحوه نمایش مجموعه چگونه است؟ در ادامه این درس میخواهیم به سوالاتی مانند این سوالات پاسخ دهیم. با ما تا آخر این درس همراه باشید.
مجموعه چیست؟
یک مجموعه در ریاضی به معنی یک گروه از اشیاء است که ویژگی مشترکی دارند. این اشیاء یا عناصر، کاملاً مشخص و غیر تکراری هستند. به عبارت دیگر، اعضای یک مجموعه باید به وضوح تعریف شوند و نمیتوانند تکرار شوند .برای این که یک مجموعه به درستی مشخص شود، اعضای آن باید به طور دقیق تعریف شوند. برای مثال، اگر بگوییم «چهار عدد زوج متوالی»، این تعریف دارای جوابهای مختلف و غیر دقیق است. به همین دلیل نمیتوان این را یک مجموعه صحیح دانست. اما وقتی میگوییم «اعداد اول یک رقمی»، این تعریف دقیقاً پنج عدد مشخص دارد:{۲, ۳, ۵, ۷}
این نکته مهم است که در مجموعهها، اعضا نباید به صورت سلیقهای انتخاب شوند بلکه باید بر اساس یک ویژگی یا قانون مشخص و دقیق تعریف شوند.
نحوه نمایش مجموعهها
مجموعهها معمولاً با استفاده از حروف بزرگ انگلیسی مانند A, B, C و … نامگذاری میشوند. اعضای یک مجموعه نیز در داخل آکولاد {} یا () قرار میگیرند.
برای مثال:
- مجموعه اعداد طبیعی یک رقمی A={1,2,3,4,5,6,7,8,9}
- مجموعه اعداد اول یک رقمی: B={2,3,5,7}
عضو بودن در یک مجموعه
برای این که یک عدد عضو یک مجموعه باشد، از نماد ∈ استفاده میکنیم. اگر عددی عضو مجموعه نباشد، از نماد ∉ استفاده میکنیم.
مثالها:
۲∈A (عدد ۲ عضو مجموعه A است)
۱۰∉B(عدد ۱۰ عضو مجموعهB نیست)
ویژگیهای مجموعهها
- ترتیب اعضای مجموعه اهمیتی ندارد:
در مجموعهها، ترتیب اعضا مهم نیست. برای مثال، {۱,۲,۳} و{۳,۲,۱} یکسان هستند. - تکرار اعضای مجموعه بیمعنی است:
اگر یک عضو چند بار تکرار شود، فقط یکبار در نظر گرفته میشود.به عنوان مثال، مجموعه {۲,۳,۵,۲,۵,۷} همان {۲,۳,۵,۷} است.
نمودار ون و نمایش هندسی مجموعهها
یکی از روشهای جالب برای نشان دادن مجموعهها، استفاده از نمودار ون است. در این روش، اعضای مجموعهها را درون یک دایره (یا منحنی بسته) قرار میدهیم. این روش به ما کمک میکند تا روابط بین مجموعهها را بصری مشاهده کنیم.
مثال:
اگرA مجموعه اعداد مرکب یک رقمی باشد، به صورت هندسی میتوانیم آن را اینطور نمایش دهیم:
A={4,6,8,9}
مجموعههای متناهی و نامتناهی
مجموعههای متناهی: این مجموعهها تعداد اعضای مشخص و قابل شمارشی دارند. به عبارت دیگر، میتوان تمام اعضای آنها را شمرد و به پایان رساند.
-
- مثال: مجموعه اعداد طبیعی دورقمی C={10,11,12,…,۹۹} :
مجموعههای نامتناهی: این مجموعهها تعداد اعضای بیپایانی دارند و نمیتوان به پایان رسید. تعداد اعضای این مجموعهها غیرقابل شمارش است.
-
- مثال: مجموعه اعداد طبیعیD={1,2,3,4,…} :
مجموعه تهی
مجموعهای که هیچ عضو ندارد، به آن مجموعه تهی گفته میشود. این مجموعه را با نماد ∅ یا {} نمایش میدهیم.
مثالها:
- مجموعه اعداد اول زوج:
C=∅
این مجموعه تهی است زیرا هیچ عدد اولی که زوج باشد وجود ندارد.
- مجموعه انسانهایی که در کره ماه زندگی میکنند:
F=∅
این مجموعه تهی است، زیرا تاکنون هیچ انسانی در کره ماه زندگی نکرده است.
مجموعههای یکعضوی
مجموعههایی که فقط یک عضو دارند، به نام مجموعه یکعضوی شناخته میشوند. این نوع مجموعهها میتوانند در حل مسائل خاص مفید باشند.
برای درک بیشتر به چند مثال از کتاب درسی صفحه ۴ریاضی نهم میپردازیم:
- مجموعه اعداد اول زوج (تنها عدد اول زوج ۲ است) G={2} .
- مجموع مضرب های اول عدد ۵ F={5}
حالا که با اصول پایهای مجموعهها آشنا شدیم، میتوانیم وارد درس بعدی شویم و مفاهیم مجموعههای برابر، زیرمجموعهها، و نمایش ریاضی مجموعهها را یاد بگیریم. در درس بعدی، یاد خواهیم گرفت که چطور دو مجموعه را با هم مقایسه کنیم، زیرمجموعهها را بررسی کنیم و مجموعهها را به روشهای مختلف نشان دهیم. پس حالا آماده باشید که در درس بعدی با این مفاهیم پیشرفتهتر آشنا شوید.
درس دوم: مجموعههای برابر و نمایش مجموعهها
در این درس، میخواهیم دو مفهوم مهم را بررسی کنیم: مجموعههای برابر و زیرمجموعهها. این مفاهیم به شما کمک میکنند که ارتباطات میان مجموعهها را بهتر درک کنید و بتوانید مجموعهها را دقیقتر مقایسه کنید. همچنین، روشهای مختلفی برای نمایش مجموعهها داریم که در این درس به آنها میپردازیم.
مجموعههای برابر
دو مجموعه زمانی برابر هستند که دقیقاً یکسان باشند، یعنی هر عضو یک مجموعه در مجموعه دیگر هم وجود داشته باشد و بالعکس. در درس دوم کتاب ریاضی نهم صفحه ۱۴ – ۴، به نحوه نمایش مجموعهها و مقایسهی آنها میپردازیم. همچنین، مفاهیم زیرمجموعه رادر این بخش بررسی میشود.
مثال:
فرض کنید دو مجموعه داریم:
A={1,3,5} B={5,3,1}
در اینجا، چون هر عضوی که در Aهست، در B هم هست و برعکس، میگوییم که:
A=B
نکته: در مجموعهها، ترتیب اعضا مهم نیست. پس حتی اگر اعضای مجموعهها به ترتیب متفاوت نوشته شوند، تا زمانی که عناصر یکسانی دارند، دو مجموعه برابرند
زیرمجموعهها
حالا میخواهیم مفهوم زیرمجموعه را بررسی کنیم. مجموعهای به نامA وقتی زیرمجموعه مجموعهB باشد، یعنی تمام اعضای A در مجموعهBهم وجود دارند. برای اطلاعات بیشتر به ریاضی نهم صفحه ۱۰ مراجعه کنید. در ادامه برای شما توضیح دادیم.
به عبارت دیگر، اگر هر عضو مجموعهA درB باشد، میگوییم:
A⊆B
مثال ۱:
- A={2,4} B={1,2,3,4}
در اینجا چون تمام اعضایA درB وجود دارند، میگوییم:
A⊆B
مثال ۲:
در اینجا چون عدد۱ازAدرB نیست، میگوییم: A⊈B
زیرمجموعه به مجموعهای گفته میشود که تمام اعضای آن در مجموعه دیگر وجود دارند، اما خود آن مجموعه برابر با مجموعه دیگر نیست. یعنی اگر مجموعه A زیرمجموعه محض مجموعهB باشد، تمام اعضای A درB هستند، ولی A≠B
مثال ۳:
در اینجا چون تمام اعضایA درB هستند، اما خود Aبرابر با Bنیست، میگوییم:
A⊂B
مجموعه تهی
ویژگی جالب: هر مجموعهای، حتی مجموعه تهی، زیرمجموعه خودش است. به این معنی که:
∅⊆A
این به این معناست که مجموعه تهی همیشه زیرمجموعه هر مجموعهای است.
تعداد زیرمجموعهها
تعداد زیرمجموعههای یک مجموعه بستگی به تعداد اعضای آن دارد. اگر یک مجموعهA دارایn عضو باشد، تعداد زیرمجموعههای آن برابر با است.
مثال ۴:
اگر A={1,2} باشد، تعداد زیرمجموعههای آن برابر با ۴ =است. زیرمجموعههایA عبارتند از:
{},{۱},{۲},{۱,۲}
مثال ۵:
اگر B={3,5,7} باشد، تعداد زیرمجموعههای آن برابر با۸=است. زیرمجموعههایB عبارتند از:
{},{۳},{۵},{۷},{۳,۵},{۳,۷},{۵,۷},{۳,۵,۷}
برای نمایش مجموعهها، دو روش اصلی داریم:
- نمایش با اعضا :در این روش، اعضای مجموعه را به طور دقیق مینویسیم.
- نمایش با ویژگیها: در این روش، مجموعه را با استفاده از یک ویژگی خاص تعریف میکنیم.
- مثال A={x∣x∈N,x<5} :
- این یعنی مجموعه A شامل تمام اعداد طبیعی کوچکتر از ۵ است..
- مثال A={x∣x∈N,x<5} :
درس سوم: اجتماع، اشتراک و تفاضل مجموعهها
در این درس، با عملیاتهای مختلفی مانند اجتماع، اشتراک و تفاضل آشنا میشویم. اجتماع دو مجموعه، مجموعهای است که تمامی اعضای هر دو مجموعه را در خود دارد، بدون تکرار. اشتراک دو مجموعه، مجموعهای است که تنها اعضای مشترک هر دو مجموعه را شامل میشود. تفاضل یک مجموعه از مجموعه دیگر اعضای مجموعه اول را که در مجموعه دوم وجود ندارند، نمایش میدهد. در ریاضی نهم صفحه ۱۶ و ۱۷، به بررسی این عملیاتها با مثالهایی از مجموعههای عددی میپردازیم
اشتراک دو مجموعه
اشتراک دو مجموعه به مجموعهای اطلاق میشود که شامل تمام اعضای مشترک آنها است. یعنی برای هر عضوی که در اشتراک دو مجموعه قرار دارد، باید هم در مجموعه اول و هم در مجموعه دوم موجود باشد.
برای مثال، فرض کنید دو مجموعه داریم:
A={4,6,8,9} B={3,5,6,8,9}
دراینجا اعضای مشترک دو مجموعه Aو B شامل ۸،۶، ۹هستند. بنابراین، اشتراک این دو مجموعه به صورت زیر خواهد بود:
A∩B={6,8,9}
به عبارت سادهتر، اگر شما دو مجموعه را داشته باشید و بخواهید اعضای مشابه آنها را پیدا کنید، باید اشتراک آنها را محاسبه کنید. اشتراک با نماد A∩B نمایش داده میشود و به این معنی است که تنها اعضایی که در هر دو مجموعه وجود دارند، در این مجموعه جدید قرار میگیرند.
اجتماع دو مجموعه
اجتماع دو مجموعه مجموعهای است که شامل تمام اعضای هر دو مجموعه است، بدون اینکه اعضای تکراری را دوباره در نظر بگیریم. به عبارت دیگر، اگر عضوی در یکی از این دو مجموعه باشد یا در مجموعه اول باشد یا در مجموعه دوم، در مجموعه اجتماع قرار میگیرد.
فرض کنید دو مجموعه داریم:
C={1,4,9,7,8,3} D={4,7,1,6,5,9}
در اینجا، تمام اعضای مجموعه Cو Dرا بدون تکرار در نظر میگیریم و مجموعه اجتماع آنها به صورت زیر خواهد بود:
C∪D={1,4,9,6,5,7,8,3}
مجموعه اجتماع با نماد A∪B نمایش داده میشود. این بدان معناست که اعضای هر دو مجموعه Aو B در مجموعه جدید قرار میگیرند و هیچ عضو تکراری در آن نیست.
تفاضل دو مجموعه
تفاضل دو مجموعه نشان میدهد که کدام اعضای یک مجموعه در مجموعه دیگر وجود ندارند. به عبارت دیگر، تفاضل A−B مجموعهای است که تمام اعضای Aکه در Bنیستند را شامل میشود.
فرض کنید دو مجموعه داریم:
A={5,6,7,8} B={7,8,9,10}
اگر بخواهیم تفاضل مجموعه A −B را پیدا کنیم، باید اعضای مجموعه Aرا که در مجموعه Bنیستند، انتخاب کنیم:
A−B={5,6}
و اگر بخواهیم تفاضل مجموعه B−A را پیدا کنیم، اعضای مجموعه B که در A نیستند را انتخاب میکنیم:
B−A={9,10}
تفاضل دو مجموعه با نماد A−B نمایش داده میشود و به این معناست که از مجموعه A، اعضایی که در B هستند، حذف میشوند.
نمایش هندسی مجموعهها با نمودار ون
یکی از راههای جذاب برای نمایش روابط بین مجموعهها، استفاده از نمودار ون است. در این نمودار، هر مجموعه به وسیله یک دایره یا بیضی نمایش داده میشود و نقاط تقاطع دایرهها نشاندهنده روابط مشترک میان مجموعهها هستند. این روش به ما کمک میکند تا بصورت بصری مفهوم اجتماع، اشتراک و تفاضل را بهتر درک کنیم.
برای مثال، فرض کنید دو مجموعه داریم:
B={5,6,7,8} A ={7,8,9,10}
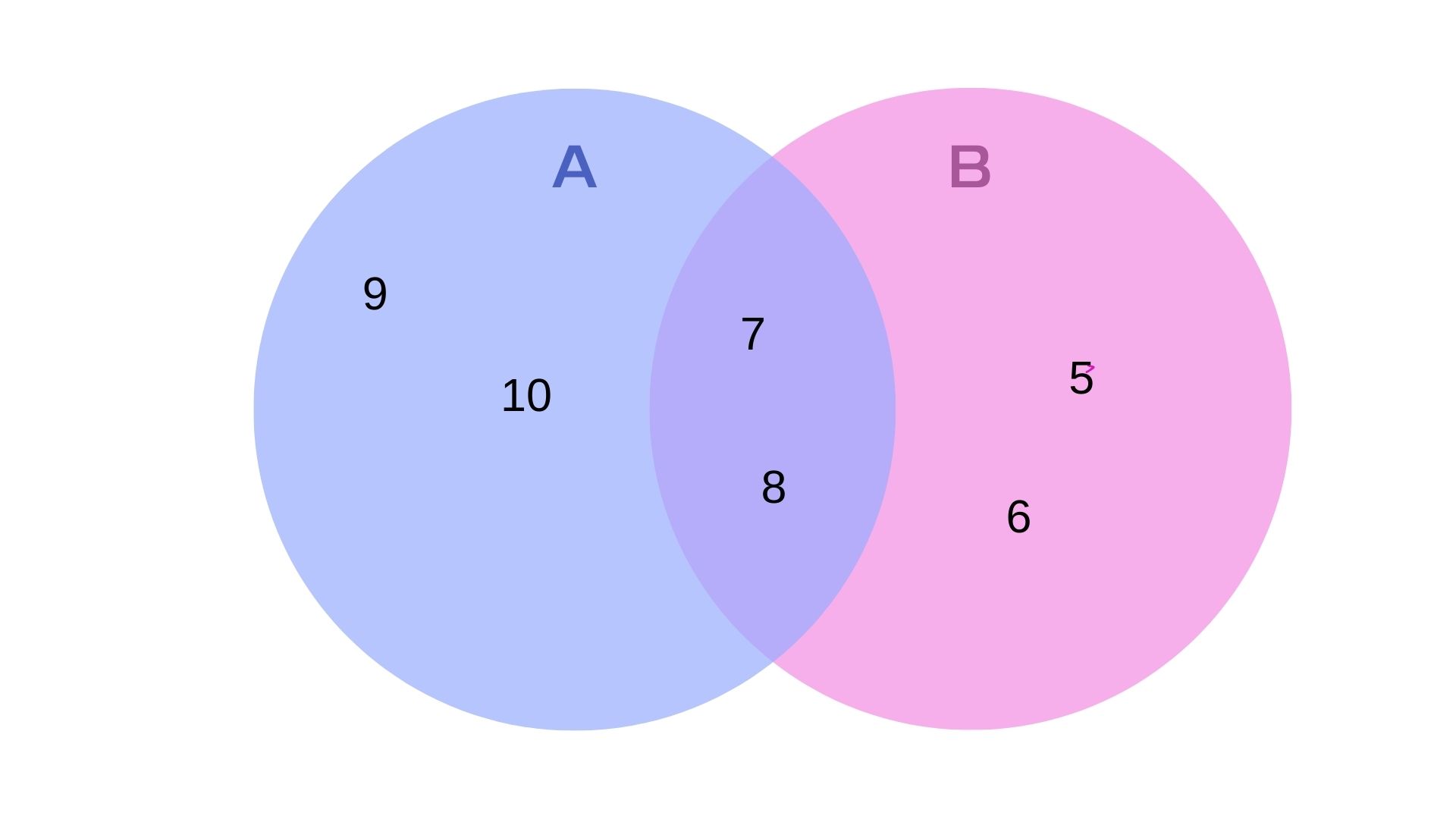
در اینجا:
- اشتراک دو مجموعه A∩B همانطور که پیشتر گفتیم:
A∩B={7,8}
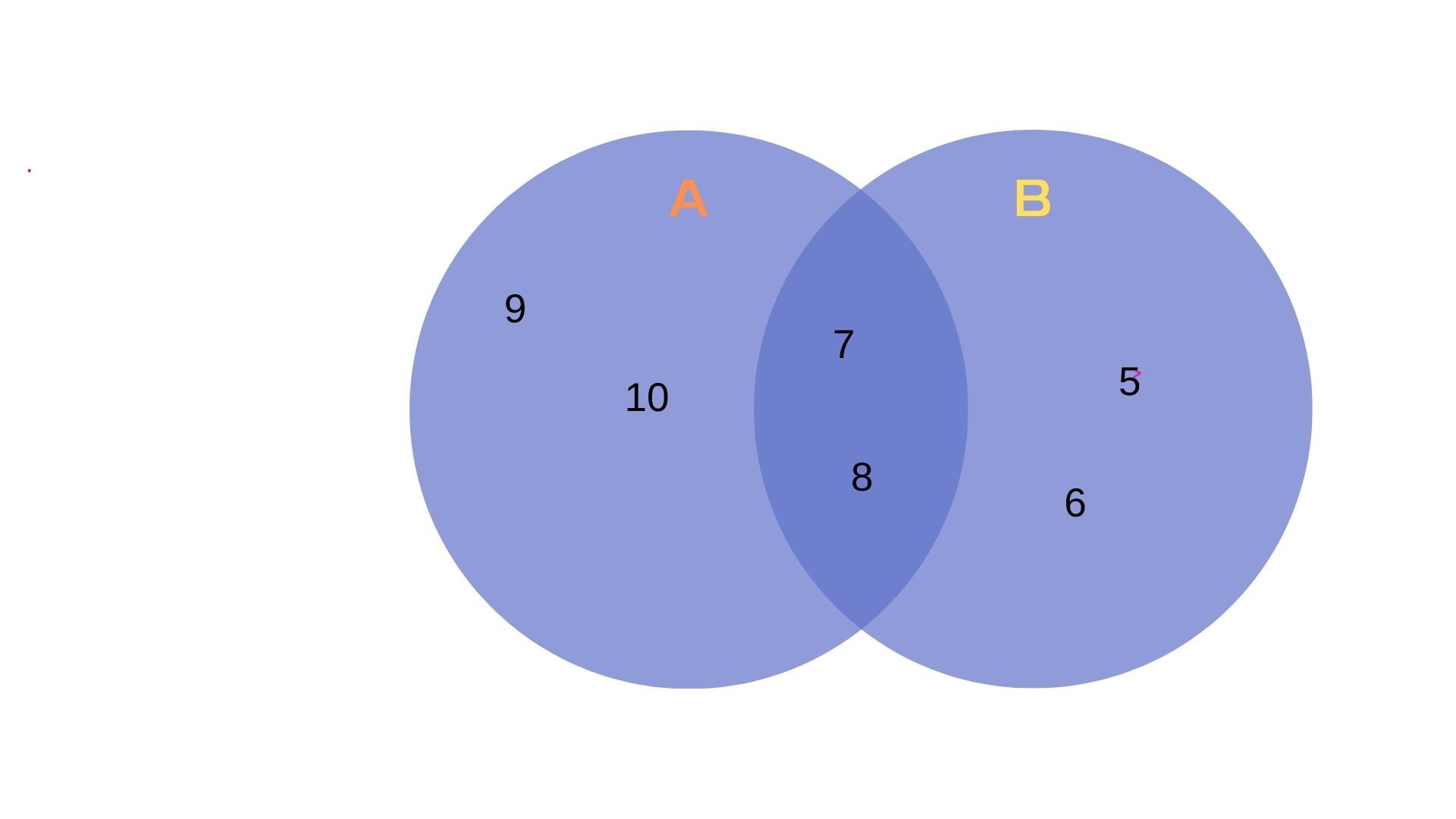
در نمودار ون، این اشتراک در ناحیهای که دو دایره A و Bهمپوشانی دارند، قرار میگیرد.
- اجتماع دو مجموعه A∪B به صورت زیر خواهد بود:
A∪B={5,6,7,8,9,10}
در نمودار ون، تمام اعضای مجموعههای A و Bدر داخل دایرهها قرار خواهند گرفت.
- تفاضل دو مجموعه A−B و B−A نیز در نمودار ون قابل نمایش است. به این صورت که اعضای مجموعه A−B در بخشی از دایره A که با B همپوشانی ندارد، و اعضای مجموعه B−A در بخشی از دایره B که با Aهمپوشانی ندارد، نمایش داده میشوند.
محاسبه تعداد اعضای مجموعهها
در ریاضیات، به تعداد اعضای یک مجموعه را با نماد n(A) نمایش میدهند و نشان میدهد که یک مجموعه چه تعداد عضو دارد.
برای مثال، اگر مجموعه A={1,2,3,4} باشد، عدد اصلی مجموعه A به صورت زیر محاسبه میشود:
n(A)=4
اگر مجموعه تهی (مجموعهای که هیچ عضوی ندارد) داشته باشیم، عدد اصلی آن برابر با صفر است:
n(∅)=۰
درس چهارم: مجموعهها و احتمال
در این درس، به معرفی احتمال و محاسبهی آن پرداخته میشود. احتمال وقوع یک پیشامد عددی بین ۰ و ۱ است که نشاندهنده احتمال وقوع یک اتفاق خاص است. با استفاده از مفاهیم مجموعهها، میتوانیم احتمال وقوع پیشامدهای مختلف را محاسبه کنیم. به عنوان مثال، احتمال وقوع یک عدد اول از مجموعه اعداد طبیعی بین ۱ تا ۱۵ را محاسبه میکنیم. برای جزئیات بیشتر، به ریاضی نهم صفحه ۱۷ مراجعه کنید.
مفهوم احتمال
احتمال هر پیشامد یا اتفاقی که ممکن است بیفتد، عددی بین ۰ و ۱ است. این عدد نشاندهنده احتمال وقوع یک پیشامد خاص است.
برای محاسبه احتمال یک پیشامد از فرمول زیر استفاده میکنیم:
P(A)=n(A)n(S)
که در آن:
- P (A) احتمال وقوع پیشامد A است.
- n(A) تعداد اعضای مجموعهای است که پیشامد A را نشان میدهد.
- n(S) تعداد اعضای فضای نمونه S است. فضای نمونه S مجموعهای است که شامل تمام حالتهای ممکن میباشد.
احتمال هر پیشامد عددی از ۰ تا ۱ است:
- اگر احتمال صفر باشد، یعنی آن پیشامد غیرممکن است.
- اگر احتمال یک باشد، یعنی آن پیشامد حتماً رخ خواهد داد.
مثالهای ساده برای محاسبه احتمال
فرض کنید یک کیسه داریم که داخل آن ۱۵ کارت قرار دارد. روی هر کارت یک عدد از ۱ تا ۱۵ نوشته شده است. حالا میخواهیم احتمال وقوع چند پیشامد مختلف را محاسبه کنیم.
فضای نمونه S
اعدادی که روی کارتها نوشته شدهاند از ۱ تا ۱۵ هستند، بنابراین فضای نمونهS به شکل زیر است:
S={1,2,3,4,5,6,7,8,9,10,11,12,13,14,15}
تعداد کل کارتها که همان تعداد اعضای مجموعهS است، برابر با ۱۵ میشود:
n(S)=15
حالا بیایید چند پیشامد را بررسی کنیم و احتمال وقوع آنها را محاسبه کنیم.
الف) پیشامد A: عدد روی کارت اول باشد.
مجموعه A شامل اعداد اول (اعداد طبیعی که فقط بر ۱ و خودشان بخشپذیرند) بین ۱ تا ۱۵ است:
A={2,3,5,7,11,13}
تعداد اعضای مجموعه A برابر ۶ است:
n(A)=6
پس احتمال وقوع پیشامد A به شکل زیر محاسبه میشود:
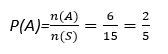
ب) پیشامد B: عدد روی کارت مرکب باشد.
اعداد مرکب (اعدادی که بیشتر از دو عامل دارند) بین ۱ تا ۱۵ عبارتند از:
B={4,6,8,9,10,12,14}
تعداد اعضای مجموعه B برابر ۷ است:
n(B)=7
بنابراین، احتمال وقوع پیشامد B به شکل زیر محاسبه میشود:
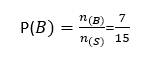
ج) پیشامد C: عدد روی کارت مضرب ۳ باشد.
مجموعه C شامل اعداد مضرب ۳ بین ۱ تا ۱۵ است:
C={3,6,9,12}
تعداد اعضای مجموعه C برابر ۴ است:
n(C)=4
بنابراین، احتمال وقوع پیشامد C به شکل زیر محاسبه میشود:
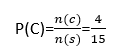
د) پیشامد D: عدد روی کارت مضرب ۱۷ باشد.
در بین اعداد ۱ تا ۱۵، هیچ عددی مضرب ۱۷ نیست. بنابراین پیشامدD غیرممکن است.
مجموعه D در این حالت برابر با مجموعه تهی است:
∅=D
تعداد اعضای D برابر ۰ است:
n(D)=0
پس احتمال وقوع پیشامد D برابر صفر خواهد بود:
![]()
حالا که محاسبات را انجام دادیم، میتوانیم نتایج زیر را بگیریم:
- احتمال وقوع پیشامد A (عدد اول باشد):
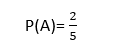
- احتمال وقوع پیشامد B (عدد مرکب باشد):
![]()
- احتمال وقوع پیشامد C (عدد مضرب ۳ باشد):
نتیجهگیری: قدرت مجموعهها در سادهسازی ریاضی و زندگی روزمره
مجموعهها در ریاضی مثل جعبههایی هستند که هر چیزی میتوانیم داخلشان قرار دهیم. با یادگیری مجموعهها میتوانیم روابط بین اشیاء و اعداد را بهتر درک کنیم. این مفاهیم به ما کمک میکنند تا مسائل پیچیده را سادهتر حل کنیم.
با مفاهیمی مثل اشتراک، اجتماع و تفاضل مجموعهها آشنا شدیم و فهمیدیم که احتمال چطور به ما کمک میکند تا شانس وقوع یک اتفاق خاص را محاسبه کنیم. این مفاهیم نهتنها در امتحانات مفیدند، بلکه در زندگی روزمره هم به کمکمان میآیند.
یادگیری مجموعهها پایهای مهم برای درک مفاهیم پیچیدهتر ریاضی است و شما را آماده میکند تا به مسائل ریاضی و حتی تصمیمات روزمره، نگاه دقیقتری داشته باشید. پس با مجموعهها، ریاضی را جذابتر و کاربردیتر یاد بگیرید!
برای شما که دانشآموز نهمی هستید: معنی درس ۱۰ فارسی نهم+ آرایه ها و جواب خودارزیابی صفحه ۷۹ و ۸